How to Manage Risk (After Risk Management Has Failed)

It is well known that over the past decade, and especially over the past few years, a number of the world’s most widely respected companies have collapsed. Analysts have cited equally well-known reasons for these collapses — the “usual suspects” of nonviable business models, greed, incompetent (and overpaid) management and a lax regulatory environment. Not often mentioned is another key consideration, something that appears to distinguish collapsed companies strongly from their noncollapsed counterparts. It is the breadth and depth of these companies’ approach to risk management.

That risk management could be a major (though not sole) cause may seem counterintuitive. The troubled American International Group Inc., for example, was a leader in risk management and even maintained a risk-management subsidiary. Its former CEO Maurice R. “Hank” Greenberg boasted that AIG had “the best risk management [departments] in the damn industry.” Bear Stearns Cos. claimed the “best-in-class processes in analyzing and managing … risk”; even the New York Times cited the company’s “carefully honed reputation for sound risk management.” Fannie Mae, the Federal National Mortgage Association, touted its “excellent credit culture and risk-management capabilities,” and Lehman Brothers Holdings Inc. prided itself on what its leaders called a “culture of risk management at every level of the firm.”1

Yet at these companies, and at others with comparable “cultures,” risk management apparently performed quite dismally. How could this be? We contend that the answer lies in the concepts and practices of traditional risk management, which tend to look for risk in all the wrong places. That is, failure did not stem from merely paying lip service to risk management or from applying it poorly, as some have suggested. Instead, collapse resulted from taking on overly large risks under the seeming security of a risk-management approach that was in fact flawed. The more extensive the reliance on traditional risk management, we believe, the greater the risks unknowingly taken on and the higher the chances of corporate disaster.

This article suggests how the key shortcomings of traditional risk management can be addressed by adopting a more sophisticated alternative — the Bayesian approach.

Not By History Alone

Two fundamentally different views have evolved over the years on how risk should be assessed. The first view — termed the objectivist, or frequentist, view — holds that risk is an objective property of the physical world and that associated with each type and level of risk is a true probability, just as there is a true atomic number for oxygen. Such probabilities are obtained from repetitive historical data, with some of the classic examples (largely for pedagogic purposes) being coin flips, die rolls and weather patterns. Based on such data, a frequentist might say that the probability of flipping a seemingly normal coin and getting heads, after having documented the results of a great many tosses, is 0.5; or that the probability of a high temperature of 95 degrees on July 4, 2011, in New York, given the extensive weather record, is 0.3.

The second view is termed the subjectivist, or Bayesian, view (named after the Reverend Thomas Bayes, an English mathematician who made major contributions to this approach during the 18th century). Bayesians consider risk to be in part a judgment of the observer, or a property of the observation process, and not solely a function of the physical world. That is, repetitive historical data are essentially complemented by other information.

Although classic cases such as coin flips come up largely in the frequentist context, they can also be used to contrast the frequentist and Bayesian views. For instance, suppose a magician pulls what appears to be a normal coin out of her pocket, allows you to flip it 10 times, and it comes up heads five of those times. She then proposes a wager based on your flipping the coin one more time and getting heads. What probability do you assign to that outcome? A frequentist presumably relies on the “historical” data from this coin (as well as from any other normal coin) and assigns a probability of 0.5. A Bayesian takes not only the data into account but also his judgment about the cleverness, trustworthiness and financial situation of the magician. He may thus assign a probability very different from 0.5 — perhaps as high as 1.0. Another observer might assign an altogether different probability, based on other judgments.

A similar argument can be made with respect to weather patterns, even where there is a great deal of repetitive historical data. For example, while the record over many decades may indicate to a frequentist that the probability of a high temperature of 95 degrees in New York City on July 4, 2011, is 0.3, a Bayesian taking an analysis of global warming into account may assign a probability that is greater than 0.3. In both cases, the historical record of the physical world is the same, but the different probabilities reflect dissimilar judgments about the present and future of that world.

Although the Bayesian view is well accepted in some circles, it has not penetrated the risk-management world. Traditional risk management has instead adopted the frequentist view, despite its three inherent, and major, shortcomings. First, it puts excessive reliance on historical data and performs poorly when addressing issues where historical data are lacking or misleading. Second, the frequentist view provides little room — and no formal and rigorous role — for judgment built on experience and expertise. And third, it produces a false sense of security — indeed, sometimes a sense of complacency — because it encourages practitioners to believe that their actions reflect scientific truth. Many of a corporation’s most important and riskiest decisions — which often do not fall into the narrow frequentist paradigm — are made without the help of the more sophisticated and comprehensive Bayesian approach.

An Exceptional Fourth Quarter

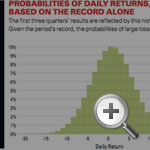
Value at Risk (VaR), arguably the centerpiece of traditional risk management, provides a good example of the limitations of the frequentist view, particularly its overreliance on historical data. The basic idea behind VaR is to calculate the potential loss within a specified time period — typically, a day. Controls then can be put in place to limit this loss to a desired level. In particular, if a company has identified a $15 million daily loss as the maximum it should tolerate, and the fourth quarter is about to begin, what is the probability of exceeding such a loss during that period? (See “Daily Returns During the First Three Quarters.”)

Using data from approximately 200 daily trials during the first three quarters of 2008, a frequentist represents the range of daily returns as a normal distribution with a mean of $1 million and a standard deviation (or volatility) of $5 million. Based on this, the probability of a daily loss of more than $15 million is extremely small, well under 0.1%. (See “Probabilities of Daily Returns, Based on the Record Alone.”) It is a less-than-one-in-1,000 event. And the probability of a daily loss of more than $25 million is infinitesimal.

The Bayesian approach, in contrast, is to look at the daily return, like all risks, as a matter of judgment that is informed by but not limited to the repetitive historical data. A Bayesian explicitly recognizes that despite three quarters (or more) of data exhibiting a volatility of $5 million, the future will not necessarily replicate the past with certainty. For example, there could be an unusual “end-of-year” effect or other (much larger) socioeconomic forces at work.

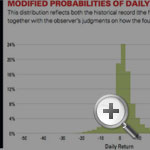
Although little, if any, repetitive historical data underlying these broader phenomena may be available, a Bayesian can quantify his judgment. For example, the analyst might see two competing phenomena: Deteriorating market conditions could cause volatility in the fourth quarter to increase, perhaps double, while newly imposed regulatory policies might cause volatility to decrease. Let us say that the Bayesian assigns a 30% chance that the volatility will remain unchanged during the fourth quarter, a 30% chance that it will double to $10 million and a 40% chance that it will be halved to $2.5 million.

As might be expected, combining this subjective information with frequency data in a seamless fashion results in an augmented distribution that is wider than the one based on the data alone. (See “Modified Probabilities of Daily Returns.”) From this distribution, the Bayesian determines that the probability of a daily loss of more than $15 million is roughly 2.0% — over 20 times that of the frequentist approach — and that the probability of a daily loss of more than $25 million is small but noninfinitesmal. (The idea of a Bayesian approach to VaR was originally suggested in 1997 and followed up in 2000 and 2004.2 It has so far gained little traction, however. Financial analyst Riccardo Rebonato’s 2007 book Plight of the Fortune Tellers: Why We Need to Manage Financial Risk Differently3 is one of the few risk-management volumes that counsel greater emphasis on a Bayesian approach.)

It is worth noting that the increase in the loss probability with the Bayesian approach is not because the Bayesian thinks that things will get worse. The increase comes because this approach formally and precisely reflects a recognition that we have limited understanding of the world and the important but nonexclusive role that frequency data play in that world. The Bayesian view makes room for judgment, quantifies that judgment in order to integrate it with data on an equal footing and acknowledges the uncertainty that inevitably remains.

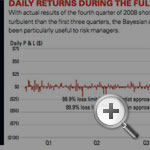
The actual daily losses for the fourth quarter of 2008, together with the 99.9% loss limits for the two approaches, would be $15 million for the frequentist approach and $27 million for the Bayesian approach. (See “Daily Returns During the Full Year.”) If such a limit is accurate, there should be only a one-in-1,000 chance that it will be exceeded in any one day. With roughly 50 “trials” in the fourth quarter, we expect that this limit should not be exceeded during that period at all. But as we now know, the fourth quarter of 2008 turned out to be a very turbulent period. Losses grew dramatically and were much more consistent with the Bayesian than the frequentist view. The frequentist limit was exceeded 15 times, while even the larger Bayesian limit was exceeded six times. Of course, this example was developed to make the point that the Bayesian view is more comprehensive and realistic. But despite the artificial construct, we believe that the broader conclusion holds. Risk management built around the reality of judgment (supported by available data) is superior to risk management built around the fantasy of fact.

Altered Rainfall Patterns?

Weather provides another example for contrasting the frequentist and Bayesian approaches to risk assessment and for highlighting Bayesian integration of data and judgment. Consider a company whose success, and possibly even existence, depends on rainfall. Such a company could be a supplier of drinking water, a hydroelectric-based energy utility, an agricultural operation or a financial enterprise with rainfall-dependent investments. Suppose 1,000 millimeters is a critical level of rainfall for the company; that is, it needs a 1,000-millimeter year at regular intervals — ideally, at least every five to 10 years. How can we assess the risk of not receiving this level of rainfall in the future?

The frequentist approach focuses entirely on the data, typically applying well-accepted statistical constructs. In this example, the rainfall pattern can be matched by a normal distribution with a mean of 880 millimeters and a standard deviation of 166 millimeters. With this distribution, the probability of rainfall of more than 1,000 millimeters in any one year is about 23%. The probability of going without a 1,000-millimeter rainfall level for five years is then (1.0 ? 0.23)⁵ or about 27%; for 10 years, about 7%; and for the 30 years between 1976 to 2005, less than 0.04%, or one in 2,500. Based on this frequentist risk assessment, one can say that the rainfall risk is extremely low.

The Bayesian approach to this issue combines, as always, the available data with judgments about the broader issues at hand. In this example, the most important broader issue is the potential effect of climate change on rainfall — a topic of considerable controversy and discussion — and a Bayesian might begin with a formal assessment of expert judgment regarding this effect.

Reflecting a great deal of uncertainty, our expert estimates that the effect of climate on rainfall ranges from a decrease of 200 millimeters per year to an increase of 100 millimeters per year. Combining this expert assessment with the historical data, we obtain a distribution for annual rainfall that is wider and shifted lower than that of the historical data alone. Specifically, the mean is 830 millimeters, and the standard deviation is 200 millimeters. Under these conditions, the probability of total rainfall greater than 1,000 millimeters in any one year is reduced to about 16%, which means that the probabilities of going without a 1,000-millimeter rainfall year during any particular time interval are quite different from those of the frequentist case: about 42% for five years, 17% for 10 years and 0.5% for all 30 years between 1976 and 2005. The latter rainfall risk indicated by the Bayesian approach is low, but not as low as the one-in-2,500 figure based on the historical data alone. In fact, this probability is more than 10 times higher.

As it turned out, the actual yearly rainfalls over the 1976 to 2005 interval were substantially lower than those of the previous 100 years. There was not a single year with rainfall over 1,000 millimeters during that 30-year period. Admittedly, this example was chosen, as the first example, to make a point. Not surprisingly, the Bayesian assessment appears to be more comprehensive and realistic. Nevertheless, we believe, as before, that a broad conclusion holds. Assessing risk by formally integrating both data and judgment leads to more useful results.

Learning, and Then Adjusting, Continuously

Another limitation of traditional risk management — that is, of the frequentist approach — involves not so much how risk is defined or measured but how it is prevented or mitigated. Because risk is assessed solely by means of the historical record, and this record changes gradually and subtly, management activity in the traditional context is largely fixed or static. It adjusts very slowly and modestly, if at all. Historical frequency data are collected to establish “the facts.” With the facts in hand, extensive rules are established and controls put in place. These controls remain essentially undisturbed until there is a serious failure or disaster, although by then it is too late. This is a rigid process, and there is no natural system for monitoring a wide range of potentially relevant events, developing insights from those events and adapting in response.

By contrast, the Bayesian perspective leads naturally to adjustments in the risk-management activity itself. Because Bayesian risk assessment combines both data and judgments, its underlying logic provides a built-in and rigorous way of updating assessments as new data arrive or new judgments emerge. Equally importantly, it provides a natural way to adjust risk-management activity in response to this learning.

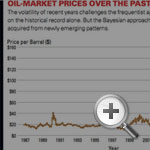
Commodity prices, such as those involving oil, provide a good example of the contrast between these two perspectives with respect to the actual management part of risk management. (See “Oil-Market Prices Over the Past 20 Years.”) The pattern has been volatile, particularly in the most recent years. Consider a company that is interested in reducing its exposure to this volatility. The typical frequentist approach is to collect as much of the oil-price data as possible and parameterize a model of the price behavior. The model can be simple, such as classic Brownian motion, or sophisticated, such as a mean-reverting Ornstein-Uhlenbeck process. Based on the model chosen, the company estimates future volatility and exposure, and it then implements an appropriate hedging strategy.

The Bayesian approach uses not only the historical data on oil prices but also accommodates judgments about the underlying factors that drive them. In particular, a Bayesian might believe that prices are influenced over the long term by two key structural drivers — global economic conditions and climate policies. As information is gained about these drivers, judgments regarding oil-price risk will change, which then leads automatically to a modified hedging strategy. (See “Learning from Recent Experience.”) The company begins with a hedging strategy for 2010 based on historical data and its judgments about the future situation. Some of the future judgments, namely, 2010 economic conditions, climate policies and oil price, are then revealed. This 2010 information serves to update judgments regarding 2011 about economic conditions, climate policies and oil price. The company then adjusts its hedging strategy for 2011 based on the revealed 2010 situation and the updated 2011 judgment. The actual 2011 situation will later be revealed too, and the hedging strategy for 2012 can similarly be adjusted in response. This updating and adjustment process continues to 2013 and beyond.

Once again, the frequentist and Bayesian approaches show themselves to be substantially different. The frequentist approach relies on a great deal of historical data. It adjusts only slowly to changing conditions, and these adjustments, such as they are, must essentially be imposed on the risk-management process. On the other hand, the Bayesian approach captures both data and judgments. It adjusts quickly to changing conditions, as well as to evolving judgments. And it is inherently dynamic — learning and adjustment are internal and automatic.

Make Room for Bayesians

The frequentist view that decisions should be based solely on facts drawn from repetitive historical data — rather than on data complemented by judgments derived from experience and expertise — can be linked to failed companies’ errors and subsequent collapse.

Why is this distinction between fact alone and fact-plus-judgment so important? First, because the fact-alone perspective provides no effective guidance on issues — often those with greatest impact — where there are little or no frequency data. It’s a classic case of losing one’s keys where it is dark but looking for them under the street lamp because the light there is so much better. Second, because unlimited faith in historical data — even large amounts of it — leads to overconfidence and excessive risk taking. And finally, because a system based solely on historical fact inevitably lurches from crisis to crisis.

The Bayesian perspective provides more accurate and powerful results. It recognizes that risk is a matter of both data and judgment, and it uses the combination in a rigorous manner for identifying, assessing and managing risk. Where there is a great deal of relevant data, this information plays a dominant role, with the integration of judgment making a substantial improvement over the traditional approach. Where there is little or no relevant data, judgment plays a dominant role, providing value under conditions beyond the scope of the traditional approach.

With the Bayesian approach, risk can be measured quantitatively, whatever the amount and quality of the data. And rather than focusing entirely on the observed world, Bayesian risk assessment also reflects the consistency, reliability and precision of the observer. Recognizing the important, sometimes central, role of judgment can lead to more reasonable and realistic behavior — in large part because we realize that judgment is not perfect and can be refined as more experience is acquired.

Admittedly, obtaining probabilities from subjective judgments rather than frequency data requires a great deal of care. The cognitive (unintentional) and motivational (intentional) biases underlying probability judgment are well known.4 For example, individuals typically exhibit considerable overconfidence in their probability assessments — that is, the distributions are too narrow. There also are well-documented biases involving the overweighting of information that is readily available and easily remembered. Fortunately, established and emerging techniques for probability encoding, such as those based on expert interviews5 and “prediction markets,”6 can reduce these biases.

The shortcomings of the frequentist view — narrowness of thinking, unwillingness to accept the possibility of error and the inability to adapt to changing circumstances — clearly played a significant role in the recent financial collapses. Companies such as Citigroup Inc. and Merrill Lynch & Co. continued to increase their exposure to subprime mortgages even as evidence regarding deterioration in the housing market accumulated: “During the early years of the housing boom, default rates on all mortgages were unusually low. That led bankers — and, more important, rating agencies — to build unrealistic assumptions about future default rates into their valuation models.”7 At these companies, early warning signs were ignored and unrealistic default rates were not adjusted until it was too late.

With a Bayesian view, such problems may not have been eliminated altogether, but they could have been substantially reduced through more comprehensive and realistic risk assessment and more dynamic and adaptive risk management. Many measures are being deployed to recover from the collapses and to build a more robust system that prevents future crises — a shift from traditional risk management to Bayesian risk management should be a part of this effort.